模糊数学评价法:定量评价休闲农业资源，实际上是在有限的范围内分配给资源对象。 该方法运用模糊数学理论和方法构建休闲农业决策模型，提出休闲农业开发价值综合评价指标。 一般而言，将评估对象抽象化为m个评估指标，可以获得一个有限域u，初步的评估工作可以获得模糊关系矩阵r，一旦被模糊变换，就可以获得评论集合上的特定综合评估子集y。
具体评价工作可分为两类:对某地区资源的综合评价和将某些地区进行共同比较的综合评价。
①单一地区综合评价:单一地区的休闲农业资源综合评价一般不直接参与该地区与其他地区资源的比较。 一般地区的休闲农业资源可以用m个具体指标来评价。 每项具体评价指标，可设n条评论。 这样，经过初步评价，得到模糊评价关系矩阵r。
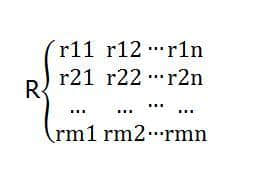中，rij是地区休闲农业资源第I项指标对第j项评论的评价。
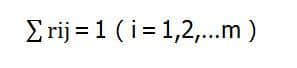符合标准化请求。
在同一地区，不同形态的休闲农业资源的作用不同，在评价过程中必须给不同的评价指标赋予不同的权重。 因此，获得属于论域u的评估权重子集A=a1，a2，am )。 其中ai是第I个评价指标的评价权重，有Σaj=1，满足正规化要求。 a和r的模型变换，可以得到属于综合评论集合v的具体评论集合y，Y=A。 y的各个分量yj表示对于某个地区的第I个评论的评价值。 yj=∨(ak∧rkj )以最大-最小法则求出。
②多地区综合评价:多地区休闲农业资源的联合评价同样可以通过论域u上的权重子集a与一个模糊关系矩阵r的模糊变换来进行。 但是，多区域资源的共同评价关系到相互的直接对比，因此需要重新设计模糊关系矩阵r。 在单独区域条件下，模糊关系矩阵是从纵向观察评价指标，在作为从横向观察的评论的多区域条件下，能够将不同的评论项目置换为不同的区域，矩阵r从纵向观察也是评价指标的第j个评论值，表示第j个区域休闲农业资源的第I个评价指标的综合 由于将评论内容抽象化，数值rij不能直接反映评论内容，因此该值可以采用直接评价的平均值rij=Σc/k。 其中，k是直接评价者的人数，Cs是第s个评价者对第j个地区休闲农业资源的第I个指标的评价。
和单一地区的评价一样，可以根据人们的消费喜好，以不同的权重给出不同的评价因素。 这样，通过权重向量a与关系矩阵r之间的变换，可以直接得到在n个地域直接比较的综合评价集y，分量yj表示第j个地域的综合评价值。
- 上一篇：总之英语的“简单地说”用英语怎么说？
- 下一篇：总之，英语-英语六级水平如何？