一尺梳理,日取一半,万世无穷。 ——庄子关于物质,我国古代庄子曾提出过上述问题。 一尺东西,今天拿一半,明天拿一半,后天拿一半,每天拿一半,真的得不到永生吗?

马拉松冠军和乌龟竞争,让乌龟先跑10公里,马拉松冠军就永远赶不上乌龟。 因为每次马拉松冠军去龟头的地方,龟又向前爬了一会儿。 ——在zenon悖论zenon悖论中,长距离竞争的优胜者无限接近乌龟,但追不上乌龟明显违反常识,从理论上来说,找到破绽是怎么回事?
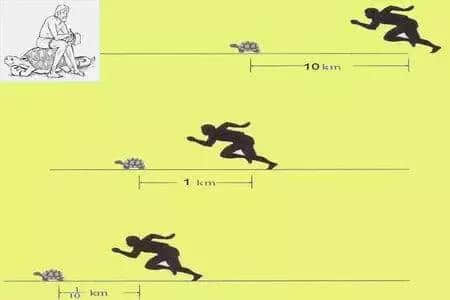
以上两个问题,一个是物质,一个是空间问题,一个是距离问题,其本质是时间问题,时间问题和空间问题是人类了解世界的基本问题,作为经验主义哲学的集大成者,休姆先从两者开始思考,休姆的思考完全可以解决这两个问题。
PS :以下是个人对休谟思想的理解,如有偏颇,欢迎指出。
人人都有时间观念,吃饭需要时间,工作需要时间,什么都需要时间,时间少一分一秒,少一秒,谁能听到这个问题:时间的本质是什么?

人人都知道时间的重要性,虽然时间很少,但他想把时间定义为下一个定义,突然觉得非常困难,是用手机跳动的数字,用手表转动的指针吗? 不,那是人类的钟表工具,是秒时、日月年吗?不,那是时间单位。 那么什么是时间呢?
休谟认为理解时间观念源于经验,当一个人经历外物的变化时,他感觉到时间,所以时间的本质是物体的变化过程。 物体从头到尾不变化,人就无法从中得到时间观念。 如果一个人永远活着,站在那里一动不动,周围的环境也没有什么变化的话,我们就会说对这个人来说,时间停止了,或者没有时间了。

人不是直接看时间,听时间才感觉到时间观念,而是根据周围环境的变化感觉到时间,所以时间不是人直接感觉到的,而是抽象观念。
人也有空间观念,但给空间下一个定义是非常困难的。 几何学上,点、线、面、身体的概念是,点开始延伸时变成线,线开始延伸时变成面,面开始延伸时变成身体,身体变成空间。
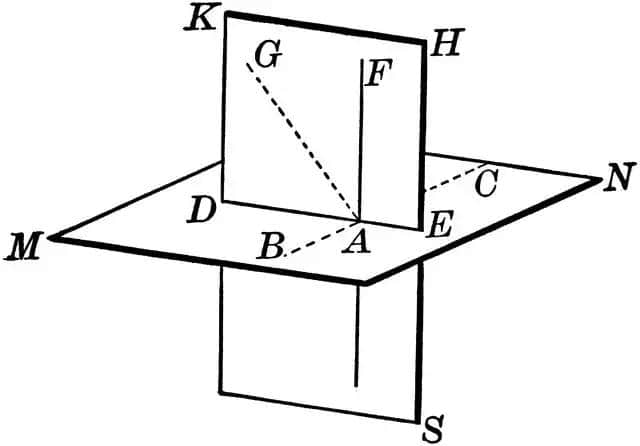
但是,休谟认为人们对点、线、面的定义也有很大的缺陷,比如线、直线是什么? 一般来说,直线定义如下:
直线由无数点构成,没有端点,两端无限延伸。 休谟认为这种定义实际上很模糊,不能理解什么是直线,为了填补这个漏洞,几何学家们指出,两点之间最短的也许就是直线,这只是直线的特征,而不是其定义,这种说法是循环论 最短是什么?要说一个人最短,他脑子里的第一印象是直线,所以把“两点之间的直线最短”翻译成“最短是最短”,能更清楚地认识到直线的概念吗?
与平面类似,平面的定义通常如下所示
这样的面,连接面上任意2点的线都落在这个面上。 或者如下所示
直线沿着水平面移动形成的路径是平面。 在这两个定义中,不是描述面的特征,而是用平面定义平面,可以看出基本点、线、面的定义不清楚。
那么人们为什么会有空间观念呢? 同样,假设人对空间观念的理解来源于经验,一个人经历外物时,他感觉到一个人大,一个人小,一个人高,一个人低,相比之下,他感觉到了空间。 和时间一样,人不是因为看到空间,接触到空间才产生空间观念,而是因为通过外物的比较感觉到空间,空间也不是人直接感觉到的,而是抽象观念。

关于时间和广告(空间),认为时间由不可分割的瞬间构成,广告由不可分割的例子构成。 换句话说,两者不是无限的,而是有各自的最小单位。 回到开头的例子,庄子认为“一尺之棣,日取其一半,万世无尽”,休谟认为物体永远不可分为两半,最后总是遇到其最小单位,可能是原子,可能是夸克,可能比夸克小,但无限分割 在芝诺悖论中,时间被无限分割,马拉松冠军追不上乌龟,休谟认为时间也不能无限分割,其最小单位可能是毫秒,也可能更小,同样,不能无限分割。
随着人类认识的发展,人类可以使物质的最小单位和时间的最小单位越来越小,这并不意味着它可以无限划分,无限划分只是数学家的游戏,数字无论多小总是可以减半,但在实际生活中,人类认识范围内的时间和空间就是这样的 休姆认为,作为经验主义者,对于既无经验又无法验证的东西,有人发誓有丹的信念。